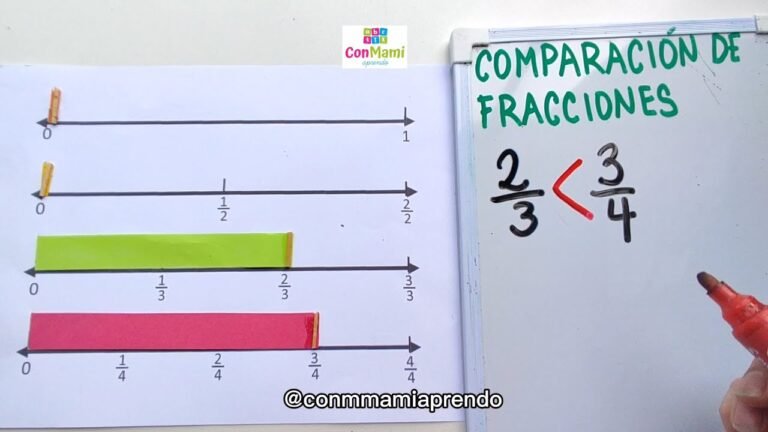
✅ Compará los numeradores tras igualar los denominadores o cruzá multiplicando: el resultado mayor indica la fracción más grande, ¡así de simple!
Para saber si una fracción es mayor que otra fácilmente, uno de los métodos más sencillos y efectivos es comparar ambas fracciones al tener un denominador común o convertirlas a números decimales. Esto permite una comparación directa y clara sin complicaciones.
Te explicaremos en detalle diferentes técnicas para determinar cuál fracción es mayor, incluyendo la obtención de un denominador común, la conversión a decimales, y otros métodos prácticos, con ejemplos claros y fáciles de seguir para que puedas aplicarlos rápidamente en cualquier situación.
Métodos para comparar fracciones fácilmente
1. Convertir las fracciones a un denominador común
Este es el método clásico y más utilizado para comparar fracciones:
- Identifica los denominadores de ambas fracciones.
- Calcula el mínimo común denominador (MCD) o mínimo común múltiplo (MCM) de estos denominadores.
- Convierte cada fracción a una equivalente que tenga el mismo denominador.
- Compara los numeradores de las fracciones resultantes: la fracción con el numerador mayor será la mayor.
Ejemplo: Comparar 3/4 y 5/6
- Los denominadores son 4 y 6.
- El MCM de 4 y 6 es 12.
- Convertimos: 3/4 = (3×3)/(4×3) = 9/12 y 5/6 = (5×2)/(6×2) = 10/12.
- Como 10 > 9, entonces 5/6 es mayor que 3/4.
2. Convertir las fracciones a números decimales
Otra forma rápida es dividir el numerador por el denominador para obtener el valor decimal:
- 3/4 = 0,75
- 5/6 ≈ 0,8333
Al comparar los decimales, se ve claramente que 0,8333 > 0,75, por lo tanto, 5/6 es mayor que 3/4.
3. Cruzar multiplicaciones para comparar sin convertir denominadores
Este método es muy útil y rápido, especialmente si no quieres calcular MCM o decimales:
- Multiplica el numerador de la primera fracción por el denominador de la segunda.
- Multiplica el numerador de la segunda fracción por el denominador de la primera.
- Compara los productos obtenidos: si el primero es mayor, la primera fracción es mayor; si el segundo es mayor, la segunda fracción es mayor.
Ejemplo: Comparar 3/4 y 5/6
- 3 × 6 = 18
- 5 × 4 = 20
- Como 20 > 18, entonces 5/6 es mayor que 3/4.
Consejos para elegir el método más adecuado
- Si los denominadores son pequeños o fáciles de manipular, usar denominadores comunes es muy claro.
- Cuando no quieres hacer cálculos largos, la cruzar multiplicaciones es el método más rápido.
- Si tienes calculadora o herramientas digitales, convertir a decimales es inmediato y visual.
Con estas técnicas, podrás determinar fácilmente cuál fracción es mayor en cualquier caso, agilizando tus cálculos y comprendiendo mejor las relaciones entre las fracciones.
Métodos prácticos para comparar fracciones con y sin denominadores iguales
Comparar fracciones puede parecer complicado, pero con algunos métodos prácticos y un poco de práctica, podés determinar cuál es mayor de manera rápida y efectiva, ya sea que tengan denominadores iguales o diferentes.
Comparar fracciones con denominadores iguales
Cuando las fracciones tienen el mismo denominador, la comparación es súper sencilla. Simplemente basta con fijarse en el numerador:
- La fracción con el numerador más grande será la mayor.
- Por ejemplo, entre 5/8 y 3/8, la fracción 5/8 es mayor porque 5 > 3.
Este método es muy útil para agilizar cálculos en problemas cotidianos o exámenes.
Comparar fracciones con denominadores diferentes
Cuando los denominadores son distintos, no se puede comparar directamente los numeradores. Aquí te dejo tres métodos prácticos:
- Reducción a denominador común: encontrar un mínimo común denominador (MCD) para ambas fracciones y convertirlas para que tengan ese denominador.
- Cruz multiplicación: multiplicar el numerador de la primera fracción por el denominador de la segunda, y viceversa, y comparar los productos.
- Conversión a decimal: dividir el numerador por el denominador y comparar los valores decimales.
Ejemplo práctico: comparación de 3/7 y 4/9
| Método | Pasos | Resultado | Conclusión |
|---|---|---|---|
| Denominador común | El MCD de 7 y 9 es 63. Convertimos: 3/7 = 27/63 4/9 = 28/63 | 27/63 vs 28/63 | 4/9 es mayor |
| Cruz multiplicación | 3 × 9 = 27 4 × 7 = 28 | 27 vs 28 | 4/9 es mayor |
| Decimal | 3 ÷ 7 ≈ 0.4286 4 ÷ 9 ≈ 0.4444 | 0.4286 vs 0.4444 | 4/9 es mayor |
Consejos prácticos para facilitar la comparación
- Usá la cruz multiplicación si querés evitar el cálculo del MCD que puede ser más engorroso.
- En situaciones de exámenes o pruebas rápidas, la conversión a decimal funciona bien, pero puede ser menos precisa por redondeos.
- Recordá que, para fracciones con denominador igual, el método es directo y rápido.
- Practicar con ejemplos variados aumenta la confianza y velocidad al comparar.
Casos de uso en la vida cotidiana
Comparar fracciones es útil para:
- Determinar qué porción de una torta es más grande entre varios invitados.
- Decidir cuál receta requiere más cantidad de un ingrediente fraccionado.
- Evaluar descuentos en porcentajes fraccionales en ofertas comerciales.
Aplicar estos métodos en contextos reales hace que el aprendizaje sea mucho más divertido y útil.
Preguntas frecuentes
¿Cómo puedo comparar dos fracciones con diferente denominador?
Encuentra un denominador común, convierte ambas fracciones y luego compara los numeradores.
¿Qué pasa si las fracciones tienen el mismo denominador?
Simplemente compara los numeradores; la fracción con el numerador más grande es la mayor.
¿Puedo usar la comparación cruzada para saber cuál es mayor?
Sí, multiplica cruzado y compara los productos para determinar cuál fracción es mayor.
¿Es útil convertir las fracciones a decimales?
Claro, convertirlas a decimales facilita ver cuál es más grande, especialmente con fracciones complicadas.
¿Qué método es más rápido para comparar fracciones?
La comparación cruzada suele ser la forma más rápida y sencilla sin necesidad de encontrar denominadores comunes.
Puntos clave para comparar fracciones fácilmente
- Cuando los denominadores son iguales, compara directamente los numeradores.
- Para denominadores diferentes, busca el mínimo común denominador (MCD) y convierte las fracciones.
- Utiliza la regla de comparación cruzada: multiplica el numerador de una fracción por el denominador de la otra y viceversa.
- Convierte las fracciones a números decimales para facilitar la comparación si las fracciones son complejas.
- Recuerda que una fracción con numerador y denominador iguales a otra siempre es igual.
- Fracciones impropias pueden ser más fáciles de comparar si las convertís a números mixtos.
¿Te resultó útil esta guía para comparar fracciones? Dejanos tus comentarios abajo y no te olvides de revisar otros artículos de nuestra web para seguir aprendiendo más sobre matemáticas y trucos fáciles.